Особый взгляд на парадокс Ферми. Часть 6. Количество обитаемых планет. Начало

— Часть 1 — Часть 2 — Часть 3 — Часть 4 — Часть 5 —
В этой части по-прежнему речь будет идти только об углеродных формах жизни, поэтому будет рассматриваться оценка количества планет, которые:
- имеют температуру, близкую к земной;
- имеют твёрдую поверхность и достаточно плотную атмосферу;
- имеют воду на поверхности.
Полагаю, имеет смысл в первую очередь рассмотреть второй из этих пунктов. Разумеется, на эти условия в первую очередь влияет размер планеты. Избыточно крупные планеты в виду способности удерживать большое количество лёгких газов — водорода и гелия — будут иметь чрезвычайно протяжённую атмосферу, постепенно переходящую в раскалённую магму без пригодной для жизни поверхности. Соответственно, главным верхним ограничением на размер обитаемой планеты будет именно наличие твёрдой поверхности, но стоит также учесть склонность к развитию парникового эффекта при избыточно плотной атмосфере, о чём подробнее следующих частях.
Нижним ограничением размера, разумеется, в первую очередь является достаточная для удержания атмосферы гравитация, но при этом следует учесть, что на сохранность атмосферы могут влиять некоторые другие факторы. Для начала стоит отметить, что влиять может как первоначальное наличие атмосферы, так и скорости потери и восполнения. Тема магнитного поля тоже будет рассмотрена отдельно. Поскольку речь идёт именно об обитаемых планетах с точки зрения углеродных форм жизни, не будем рассматривать варианты с вымерзанием атмосферы и различного состава последней в зависимости от температуры. Речь будет идти именно о веществах, находящихся в газообразном состоянии при земной температуре.
О первоначальном наличии атмосферы будет сказано подробнее в следующих частях, пока что будем считать вероятность наличия очень высокой, и рассмотрим факторы потери атмосферы. Сперва стоит заметить, что потеря атмосферы происходит, когда молекулы соответствующих газов получают скорость более второй космической для рассматриваемой планеты. Поэтому имеет смысл делать оценки исходя из гравитации, задающей вторую космическую скорость, и факторов, влияющих как на среднюю, так и на пиковую скорость движения молекул газов.
Как известно, средняя энергия молекул идеального газа составляет 3/2kT, где k — постоянная Больцмана, T — абсолютная температура. Поскольку в виду отсутствия ряда важных данных, например, о геологической активности экзопланет, вряд ли возможно точно оценить все факторы, например, состав и скорость восполнения атмосферы, ограничимся рассмотрением идеального газа, поскольку эта погрешность на точность общих результатов сильно не повлияет. В итоге средняя скорость молекул равна
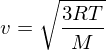
где М — молярная масса, R — молярная газовая постоянная. Например, для земного воздуха в среднем М = 0,029 кг/моль, поэтому при +20°C средняя скорость молекул составит около 500 м/с, что гораздо меньше второй космической скорости нашей планеты. Но следует учесть, что, во-первых, земной воздух не является однородным веществом, молекулы разных газов будут иметь разную скорость, во-вторых, возможны локальные колебания температуры, в третьих — средняя скорость может быть существенно меньше пиковой.
Вероятность изменения скорости молекулы на dv по сравнению со средней по нормальному распределению P(dv) будет пропорциональна величине
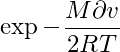
Нормировка по вероятности будет выполняться при коэффициенте
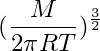
т. е. вероятность заданной скорости v + dv в заданный момент времени будет равна
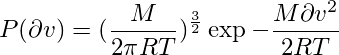
Для вычисления вероятности изменения скорости не менее, чем на dv, понадобится интеграл
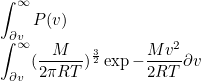
Этот интеграл не записывается в аналитической форме, но, поскольку речь идёт о низких вероятностях, по приблизительной оценке степень интегральной функции будет примерно в два раза меньше. Рассмотрим именно эту примерную оценку, а также в предельно упрощённом варианте можно рассмотреть длину свободного пробега молекулы как расстояние движения с постоянной скоростью. При плотности ρ количество молекул в единице объёма составит
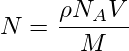
где N A — постоянная Авогадро, M — молярная масса. Отсюда среднее расстояние между молекулами будет
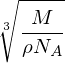
При плотности воздуха 1 кг/м3 и его молярной массе 0,029 кг/моль среднее расстояние между молекулами составит около 3,6 нм. При рассмотренной ранее скорости движения молекул в среднем изменение скорости будет происходить за 7,2 пс.
В итоге получается, что отличие скорости молекулы на 100 м/с будет иметь вероятность около двух миллионных долей, соответственно, когда в одном кубическом метре воздуха будет около 20 секстиллионов молекул, в течение одной секунды не меньшая скорость хотя б у одной молекулы будет наблюдаться в среднем около 5 октиллионов раз. Разница до второй космической скорости для земли будет больше приблизительно в 100 раз, соответственно, разница составит около 260 порядков, т. е. количество секунд, за которое одна молекула будет в среднем покидать атмосферу земли подобным способом, будет иметь более 110 нулей. Это пример рассмотрения одного из перечисленных факторов. Легко заметить, что при пиковом нагреве до 1000К молекулы водорода и атомы гелия будут иметь среднюю скорость около 4 км/с, а доля молекул, имеющую вторую космическую скорость, составит около десятимиллиардной доли. При плотности около 1 мкг/м3 среднее изменение скорости будет происходить в среднем примерно за 1 нс, количество молекул в кубическом метре будет несколько десятков триллионов, значит, в среднем за секунду в одном кубическом метре 10 млрд молекул будут покидать атмосферу. Около 10 минут пикового нагрева хватит для потери 99% водорода и гелия, что, разумеется, относится лишь к верхнему слою атмосферы, но даже из такой очень приблизительной величины ясно, что в течение хотя б нескольких миллионов лет это закончится почти полной потерей водорода и гелия в атмосфере.
Указанная пиковая температура для верхних слоёв атмосферы нашей планеты вполне возможна, например, в моменты вспышек на солнце, о них и прочих факторах подробнее в следующих частях. Для азота по аналогичной очень приблизительной оценке при 1000K для потери 1% потребуется более нониллиона лет. Даже с такой низкой точностью появляется возможность предсказать наличие тех или иных газов в атмосферах планет в зависимости от второй космической скорости. Например, вторая космическая скорость Марса в 5 км/с очевидным образом гарантирует очень быструю потерю водорода и гелия, а для азота в моменты нагрева до 1000К средняя скорость составит около 950 м/с для молекулярного и 1,3 км/с для атомарного. В итоге даже для молекулярного азота приблизительно квинтиллионная доля молекул будет иметь вторую космическую скорость, а для атомарного значение достигнет почти триллионных долей. В секунду будет теряться где-то около миллиардной доли молекул азота, что позволит за суммарные 30 лет пикового нагрева потерять около половины азота. Из этого можно сделать вывод, что через несколько миллиардов лет азота почти не останется.
По такой примерной оценке вторая космическая скорость от 8 км/с может обеспечить сохранность достаточного количества азота, а вторая космическая скорость более 30 км/с почти гарантирует, что планета будет газовым гигантом. Если ограничиться рассмотрением углеродных форм жизни, то именно этот диапазон имеет смысл рассматривать для потенциально пригодных для жизни планет. На особенности атмосферы влияет множество факторов, но в следующих частях будет рассмотрен вопрос, почему именно величина второй космической скорости может использоваться для оценки пригодности атмосферы планеты для жизни.
В сильно упрощённой форме вторую космическую скорость можно представить как
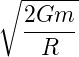
где G — гравитационная постоянная, m — масса планеты, R — радиус планеты, или в ещё более упрощённой форме как
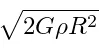
где ρ — средняя плотность планеты. Для приблизительной оценки распределением массы и плотности можно пренебречь. Поскольку речь идёт о потенциально обитаемых каменистых планетах, имеет смысл предполагать незначительное увеличение плотности с увеличением радиуса. Тогда примерная оценка минимального радиуса составит около 5 тыс. км., а максимального 15 — тыс. км. В первом случае ускорение свободного падения может составить около 7 м/с2, во втором — превышать 30 м/с2 в зависимости от распределения плотности.
В следующих частях рассмотрим другие параметры потенциально обитаемых планет.





